An Angelic Aspect of The Cauchy Distribution

In statistical literature, the Cauchy distribution is often branded as "evil" or "pathological" because it lacks well-defined mean, variance, or any higher-order moments. As a result, it is frequently used as a counterexample to demonstrate the breakdown of certain statistical laws, such as the Central Limit Theorem and the Law of Large Numbers - and has otherwise seen limited practical use. Interestingly, a recent publication by Liu and Xie (2020) uncovers an angelic side of this distribution, revealing its potential application in clinical trials through the so-called Cauchy combination test (CCT).

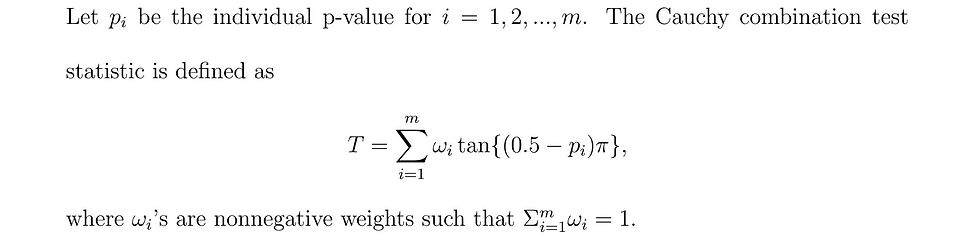
Under the null hypothesis, 𝑝ᵢ is uniformly distributed on [0, 1], and thus each component 𝑡𝑎𝑛{(0.5-𝑝ᵢ)π} in the combination test follows a standard Cauchy distribution. Additionally, if the 𝑝ᵢ's are independent then it's easy to see that the test statistic 𝛵 also follows a standard Cauchy distribution. This conclusion, however, does not necessarily hold for correlated 𝑝ᵢ's (except for a perfect correlation). While the correlation affects the null distribution of the CCT, Liu and Xie (2020) proved that its impact on the tail distribution is rather limited. Specifically, they showed that under the null hypothesis and any correlation structure among the 𝑝ᵢ's, the test statistic 𝛵 has an approximate Cauchy tail. That is,

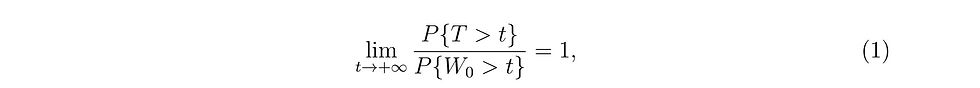
where 𝑊₀ denotes a standard Cauchy random variable.

The result in Equation (1) suggests that, despite the correlation among the 𝑝ᵢ's, we can reliably use the standard Cauchy distribution to approximate the tail distribution of the CCT. If we observe 𝛵 = 𝑡₀, then the p-value of the test statistics can be approximated by

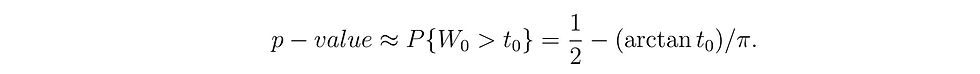
As noted earlier, this approximation becomes exact when the 𝑝ᵢ's are independent. It is also evident that the smaller the individual p-values, the larger the 𝛵 value, and the more accurate the approximation is expected to be. Two apparent advantages of the CCT are:

1. Simple p-value calculations: The calculations involved are easy and straightforward.

2. Broad applicability: The test can be used regardless of the correlation structure among the individual p-values.

Potential applications of the CCT in clinical trials include:

• Multiplicity control: Combining p-values from multiple tests to obtain an overall p-value for testing a global null hypothesis.

• Multiple imputation: Deriving a combined p-value from individual p-values calculated across the multiple imputed datasets.

• Adaptive design: Similar to other p-value combination methods, such as Fisher's combination test.

  Note that, however, Fisher's combination test requires independent p-values.

It is important to note that, in certain situations, the CCT may be less powerful compared to some other methods. Therefore, it is advisable to carefully evaluate the performance of different approaches before applying them.

References

Lin, Y. and Xie, J. (2020). Cauchy combination test: a powerful test with analytic p-value calculation under arbitrary dependency structures. Journal of the American Statistical Association 115 (529), 393-402.