Analysis of Covariance: Correlated Covariates

This post continues our previous discussions on statistical issues related to analysis of covariance (ANCOVA), focusing on the impact of the correlated covariates. Correlated covariates in an ANCOVA model can be concerns for some statisticians, often due to a lack of thorough understanding of the variance inflation caused by collinearity, a well-known phenomenon in regression analysis. Specifically, when variance inflation occurs, it affects only the correlated covariates and does not impact variables that are independent of others (this is true for general linear models). In simple terms, variance inflation is an "epidemic" confined to the correlated covariates, rather than a "pandemic" affecting the entire model. Therefore, the presence of correlated covariates in an ANCOVA model should not be a concern as long as the primary focus is on the effect of treatment (assuming no correlation between the treatment and covariates), as is typically the case in clinical trials. The following simulations provide numerical evidence to support this point.

Consider a clinical trial with a continuous response variable, two treatment groups, and three potential continuous covariates. To generate data, we assume the response variable and the three covariates jointly follow a multivariate normal distribution with the following covariance matrix

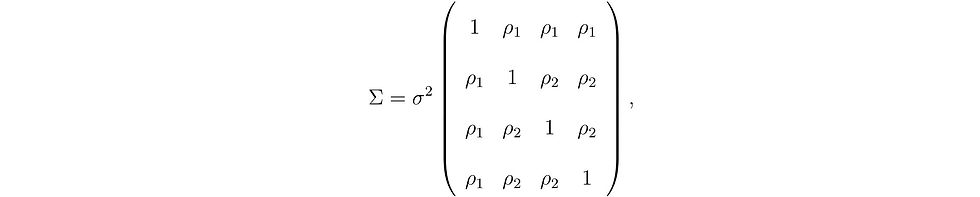
where 𝜎² is a common variance (for simplicity) for the response variable and the covariates, ρ₁ stands for the correlation between the response and each covariate, ρ₂ the correlation between each pair of the covariates. This structure implies that the three covariates are equally informative for the response. The following settings are used for simulations:

• sample size 𝑛 = 20 per treatment group

• treatment group difference ∆ = 1

• 𝜎² = 1, ρ₁ = 0.7, and ρ₂ = 0.5, 0.75, 0.99.

ANCOVA is performed on each simulated dataset using models with a single covariate (Model 1, which serves as the reference), two covariates (Model 2), and three covariates (Model 3) separately. The least-squares (LS) estimate of the treatment difference (Difference) and its standard error (StdErr) are obtained from each ANCOVA model. Simulations are conducted using the SAS GLM procedure with 20000 replications for each scenario. The following table presents the mean values of Difference and StdErr, as well as the range of StdErr based on the 20000 replications.

It's easy to observe the following:

1. Regardless of the strength of the correlation ρ₂, the mean values of the LS estimates of the treatment difference from the three ANCOVA models are very close to the true value of ∆ = 1.

2. Including additional covariates correlated with the response generally improves efficiency in the treatment group comparison, provided they are not strongly correlated with each other.

3. Any efficiency loss due to strongly correlated covariates is likely to be limited, unless a large number of redundant covariates are included.

Additionally, it can be shown that in the extreme case where ρ₂ = 1 (i.e., perfect collinearity), all three ANCOVA models will yield identical results for the treatment group comparison.

We conclude that the presence of strongly correlated covariates does not pose a major concern when estimating the treatment effect, though inferences about the covariates themselves may be impacted by collinearity.