A recent LinkedIn post by a fellow statistician caught my attention. The author touted the appealing concept of NNT, which is widely understood, but apparently overlooked a serious statistical issue it presents: the commonly used naive estimator for NNT has an ill-behaved (pathological) distribution, making it particularly challenging to draw valid statistical inferences. Sadly, in my opinion, the use of NNT in medical research has become one of many poor practices adopted by medical professionals, including biostatisticians.
In the context of a clinical trial with binary responses (assuming a higher response rate is better), NNT is defined as:
where 𝑝₁ and 𝑝₂ are the true response rates for the control and treatment groups respectively. NNT can be defined as infinity (∞) if 𝑝₁ = 𝑝₂. A naive estimate of NNT is given by
where 𝑝̂₁ and 𝑝̂₂ are the unbiased estimates (sample proportions) of 𝑝₁ and 𝑝₂ respectively.
The statistic 𝑝̂ = 𝑝̂₂ - 𝑝̂₁ has an asymptotic normal distribution with mean 𝑝 = 𝑝₂ - 𝑝₁ and variance, say, 𝜎ₚ² > 0. As a result, the variable Υ = 1/𝑝̂ has an asymptotic distribution with a probability density function 𝑓(𝑦) of the form
It should be noted that the domain of 𝑓(𝑦) is 𝑦 ∈ (-∞, +∞) although practically Υ = 1/𝑝̂ ∉ (-1, 1). It can be verified that 𝑓(𝑦) is in general very close to 0 for 𝑦 ∈ (-1, 1), so the restriction of Υ ∉ (-1, 1) is not an issue for the validity of the asymptotic distribution. The following figure shows two different density functions: 𝑝 = 0 (red curve) and 𝑝 = 0.1 (blue curve), both with 𝜎ₚ = 0.12.
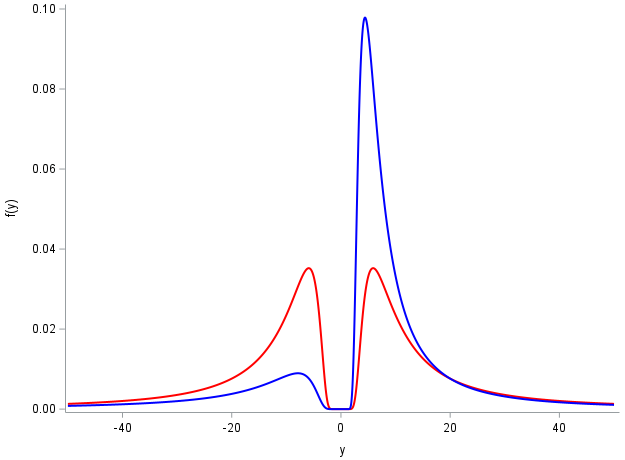
The distribution 𝑓(𝑦) has the following properties:
It is symmetric if 𝑝 = 0, and asymmetric otherwise.
It has no well-defined mean, variance or higher-order moments.
It has a positive median for 𝑝 > 0, a negative median for 𝑝 < 0, and a median = 0 for 𝑝 = 0.
It has two modes at 𝑚₁ = [-𝑝-√(𝑝²+8𝜎ₚ²)]/(4𝜎ₚ²) and 𝑚₂ = [-𝑝+√(𝑝²+8𝜎ₚ²)]/(4𝜎ₚ²).
An appropriate measure of the central tendency of this distribution is one of the two modes (if 𝑝 ≠ 0), representing the region from which the sample value of Υ = 1/𝑝̂ is likely drawn. If Υ = 1/𝑝̂ is indeed a "good" estimate of NNT = 1/𝑝, we should expect either 𝑚₁ ≈ 1/𝑝 or 𝑚₂ ≈ 1/𝑝. Let's examine if this is the case.
If 𝑝 = 0, then the two modes are located at ±1/(𝜎ₚ√2). In this case, neither mode is close to 1/𝑝 (NNT = ∞) for any given 𝜎ₚ > 0.
If 𝑝 > 0, then we consider the positive mode 𝑚₂. It is easy to see that
where the approximation is obtained using the first-order Taylor expansion of the function √(1+𝑥)
assuming that 𝑥 = 8𝜎ₚ²/𝑝² < 1. This approximation becomes more accurate as 𝜎ₚ²/𝑝² approaches 0
(i.e., 𝜎ₚ ≪ 𝑝). For example, if 𝑝 = 0.1 and 𝜎ₚ = 0.01 (𝜎ₚ²/𝑝² = 0.01) then 𝑚₂ = 9.81, which is very
close to NNT = 10. In general, 𝑚₂ < 1/𝑝 holds for any 𝑝 > 0 and, in addition, 𝑚₂ ≪ 1/𝑝 if 𝜎ₚ²/𝑝² is
sufficiently large (𝑝 ≪ 𝜎ₚ). So, in the case of 𝑝 > 0, 𝑚₂ ≈ 1/𝑝 holds true only if 𝜎ₚ²/𝑝² is sufficiently
small (i.e., close to 0).
Similarly, for 𝑝 < 0, 𝑚₁ ≈ 1/𝑝 holds true only if 𝜎ₚ²/𝑝² is sufficiently small.
It can also be shown that the median ≈ 1/𝑝 holds true only if 𝜎ₚ²/𝑝² is sufficiently small. These results indicate that the distribution of Υ = 1/𝑝̂ is concentrated around 1/𝑝 only when 𝜎ₚ²/𝑝² ≈ 0. As a result, the statistic Υ = 1/𝑝̂ may provide a "good" estimate of 1/𝑝 only if 𝜎ₚ²/𝑝² is sufficiently small.
Subsequent challenges include evaluating the performance of the estimate Υ = 1/𝑝̂ and conducting hypothesis testing. Specifically, how "good" (reliable) is this estimate, and how can we construct a valid test statistic for it? These questions are generally difficult to address due to the pathological distribution of Υ = 1/𝑝̂.
While we embrace simple statistical concepts, it's crucial to remember that simplicity alone should never outweigh statistical rigor or compromise the integrity and interpretability of statistical inferences. Who would need the Box-Cox transformation otherwise?
Comments